
Правильное управление средствами. Колебания банкролла при преимуществе игрока. Выборка ставок.
Умение управлять банкроллом и понимать, как на него влияют отклонения, – жизненно необходимые навыки для делающих ставки игроков. В чем заключается взаимосвязь между коэффициентами, преимуществами и отклонениями? Какие закономерности в изменении банкролла можно проследить при изменении коэффициентов? Читайте дальше и узнайте ответы на свои вопросы.
Благодаря возможности спрогнозировать исход серии ставок и эффективному управлению банкроллом игрок сможет избежать влияния определенных поведенческих искажений, таких как: чрезмерная уверенность, склонность приписывать себе успехи и «иллюзия навыка», способных свести на нет ожидаемую долгосрочную прибыль. В этой статье рассматривается взаимодействие коэффициентов, преимуществ и отклонений, а также приводятся рекомендации по формированию ожидаемого банкролла для размещающих ставки игроков.
Управление банкроллом
Умение управлять банкроллом и осознавать влияние на него отклонений являются крайне важными навыками для любого размещающего ставки игрока. От игры в покер и до размещения ставок на результаты спортивных состязаний: в список навыков успешного игрока в любой сфере должна входить способность распознавать наличие преимущества и определять его величину, а также умение учитывать отклонение, создаваемое удачей или неудачей.
Рассмотрим ставку, размещаемую с коэффициентами, составляющими 2,0, что предполагает равную 50 % (при отсутствии маржи) вероятность благоприятного исхода. Если игрок сможет точно определить, что истинная вероятность равна 52 % (объективные коэффициенты равны 1,92), то ожидаемая прибыль каждой ставки, размещенной с коэффициентами, равными 2,0, составит 4 % (2,0 / 1,92 – 1). Назовем эту величину «преимуществом» игрока.
Давайте предположим, что игрок вступает в игру с банкроллом, равным 100 единицам, и размещает ставку, эквивалентную одной фиксированной единице. После размещения 100 таких ставок банкролл игрока будет составлять величину в диапазоне от 0 до 200 единиц, тем не менее ожидаемый размер банкролла равен 104 единицам — прибыль в размере 4 %.
Проведя симуляцию этого сценария 10 000 раз, мы сможем увидеть влияние отклонений на суммарный банкролл игрока (см. диаграмму ниже).
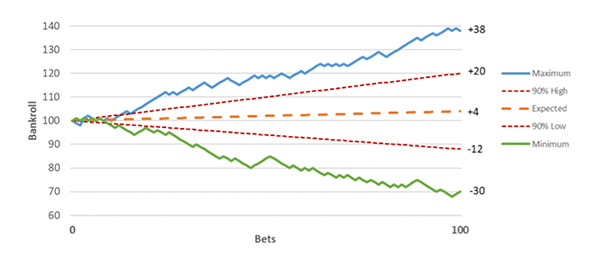
Понимание отклонений
Несмотря на то, что средний результат представляет собой увеличение банкролла на 4 единицы, мы можем также наблюдать существенную разницу между наилучшим (+38 единиц) и наихудшим (–30 единиц) исходами. Для игрока крайне важно понимать то, как работает отклонение, и осознавать, что преимущество в 4 % не гарантирует 4%-ную прибыль.
В 90 % случаев симуляции размещения 100 ставок игрок может ожидать прибыль в диапазоне от –12 до +20 единиц. Просадка на 10 единиц (при использовании начального банкролла) может ожидаться в 20 % случаев, тем не менее только в 2 % случаев игрок столкнется с просадкой на 20 единиц.
Любопытен тот факт, что в 32 % случаев банкролл игрока может уменьшиться после размещения 100 ставок, невзирая на наличие 4%-ного преимущества для каждой ставки.
Если мы увеличим преимущество игрока до 10 % (истинная вероятность составит 55 % для размещения ставки при коэффициентах, равных 2,0), к убыли банкролла после размещения 100 ставок приведет только 13 % случаев.
Профессиональный USDT Букмекер и Казино с повышенной отдачей (до 99%). Узнать подробнее
Вероятность просадки на 20 или более единиц составляет всего 0,4 %. Вполне очевидно, что при увеличении преимущества вероятность неудачного исхода уменьшается, но что же произойдет, если количество размещаемых ставок увеличится до 5000? На диаграмме внизу показан первый из приведенных выше сценариев (истинная вероятность равна 52 %, коэффициенты для размещения ставок составляют 2,0), симуляция проводилась 10 000 раз.
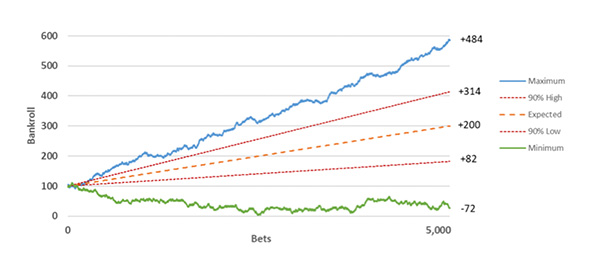
Пусть худший исход и составил целых –72 единицы, только 28 (0,28 %) из проведенных 10 000 симуляций показали убыль банкролла после размещения 5000 ставок. В 90 % симуляций была сгенерирована прибыль в диапазоне от +82 до +314 единиц. Таким образом, доходность ставок (ROI) колеблется от 1,64 % до 6,28 %.
Как изменится этот сценарий, если вместо равных 2,0 коэффициентов использовать коэффициенты, составляющие 4,0 (предполагаемая вероятность равна 25 %)? Если мы установим, что истинная вероятность соответствует 26 % (объективные коэффициенты равны 3,846), то ожидаемая прибыль сохранит свою величину в размере +4 % (4,0 / 3,846 – 1), однако каким же образом изменится отклонение?
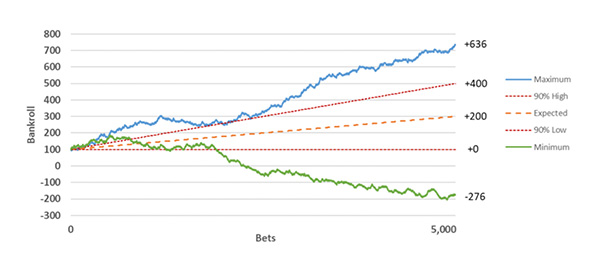
Как сравнить диаграммы?
При сравнении двух графиков мы можем заметить, что, несмотря на одинаковый размер и количество ставок, а также на сохранение величины ожидаемой прибыли, отклонение значительно увеличивается. Среднеквадратическое отклонение прибылей возрастает с 1,4 % до 2,4 %. Величина разброса результатов симуляции на 64 % больше для того сценария, в котором коэффициенты для ставок равны 4,0, а 90%-ный доверительный интервал шире на 72 %, что соответствует ожидаемой доходности в диапазоне 0–8 %.
В первом сценарии игрок потеряет все 100 единиц банкролла только в 2 случаях из 10 000 симуляций (0,02 %). Во втором сценарии все 100 единиц банкролла оказываются утраченными в 6,3 % симуляций. Просадка на 50 единиц гораздо более вероятна (25,7 %) при размещении ставок на аутсайдера с коэффициентами, равными 4,0, чем при использовании эквивалентных 2,0 (2,0 %) коэффициентов.
В наихудшем случае размещения ставок при коэффициентах, равных 4,0, может быть утрачен практически троекратный банкролл (–276 единиц). На этом примере мы можем понять, что при фиксированном размере ставки, количестве ставок и ожидаемой прибыли величина отклонения будет расти вместе с увеличением коэффициентов.
Таким образом, игрок, который размещает большинство своих ставок на аутсайдеров, может ожидать большее количество и больший размер колебаний банкролла, чем игрок, размещающий ставки на фаворитов, даже если оба они обладают одинаковым преимуществом.
Учитывая тот факт, что для размещения 5000 ставок на результаты спортивных состязаний обычному игроку понадобятся месяцы или даже годы, возможно, стоит в первую очередь разобраться в закономерностях изменения банкролла для гораздо меньшего количества ставок.
Исходя из предположения, что игроку удастся найти 4%-ное преимущество при коэффициентах, равных 2,0, а кроме того, он сможет размещать фиксированные ставки размером в одну единицу, можно составить диаграмму, подобную расположенной ниже: на ней указана вероятность на просадку стартового банкролла на определенное количество единиц в результате размещения серии, состоящей из 100–1000 ставок (результаты рассчитаны на основе 10 000 симуляций).
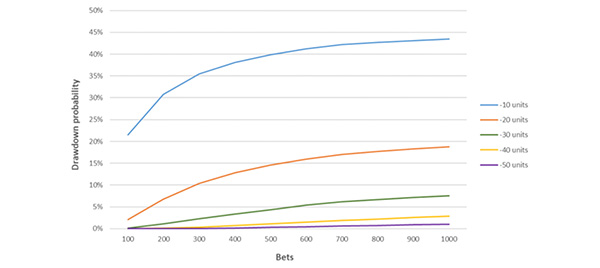
Размещая 1000 ставок при коэффициентах, равных 2,0, и преимуществе, составляющем 4 %, мы приближаем вероятность просадки определенной величины к ее верхнему пределу (в особенности это касается просадок меньшей величины). С увеличением преимущества игрока снижается шанс определенной просадки. На диаграмме ниже приведены вероятности для 1000 ставок при коэффициентах, равных 2,0, результаты рассчитаны на основании 10 000 симуляций.
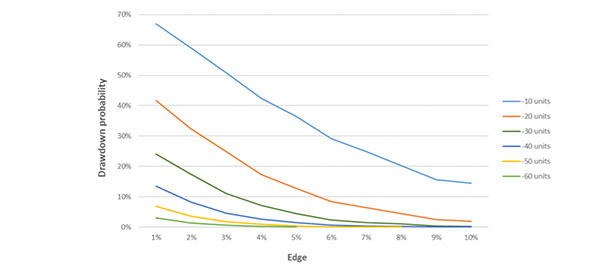
Например, при наличии 4%-ного преимущества шанс просадки банкролла на 20 единиц по результатам размещения 1000 ставок с коэффициентами, равными 2,0, составляет 17,4 %. Однако же шанс на потерю 20 или более единиц после размещения 1000 аналогичных ставок равен всего 2,8 %. Понимание подобных различий позволит игроку рассматривать свое долгосрочное преимущество сквозь призму краткосрочных отклонений.
Различные закономерности в изменении банкролла
Как изменится банкролл при постоянных размерах ставок и преимуществ, но с учетом непостоянства коэффициентов? Диаграмма ниже показывает вероятность различных просадок (в сравнении с начальным банкроллом) при размещении 1000 ставок по одной единице с различными коэффициентами игроком, обладающим преимуществом в 4 %. Симуляция каждой серии из 1000 ставок была выполнена 10 000 раз.
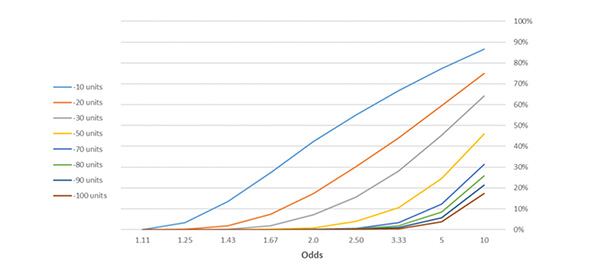
Давайте вспомним, что при размещении ставок с коэффициентами величиной в 2,0 мы имели 17,4%-ную вероятность потери 20 единиц на определенном этапе серии из 1000 ставок. При равных коэффициентах, равных 5,0, вероятность просадки величиной в 20 единиц возрастает практически до 60 %. Даже при неизменности размера ставок, преимущества и ожидаемой от серии ставок прибыли в размещении преимущественного числа ставок на фаворитов и на абсолютных аутсайдеров работают совершенно разные по масштабам отклонения закономерности.
Таким образом, понимание того, к какому типу игроков вы относитесь, является критически важным для умения справляться с последствиями, которые вас постигнут.
Для того чтобы подсчитать подобное отклонение, давайте снова рассмотрим серию из 1000 ставок. Приведенная ниже диаграмма демонстрирует среднеквадратическое отклонение прибыли с учетом изменения коэффициентов (предполагаемая вероятность колеблется в пределах от 10 до 90 %) и преимущества.
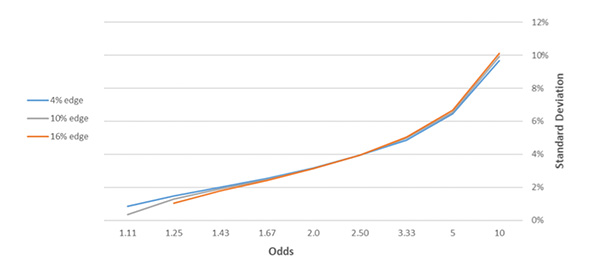 Мы можем отчетливо наблюдать увеличение отклонения при увеличении коэффициентов (или же при снижении предполагаемой вероятности), что соответствует ранее проведенному анализу. На диаграмме выше показаны результаты для размещения 1000 ставок по 1 единице, с 10%-ным преимуществом, со среднеквадратическим отклонением величиной в 6,5 % и с учетом предположения, что все ставки размещаются с коэффициентами величиной в 5,0; сравнение выполняется с 2,5%-ным преимуществом и коэффициентами в размере 1,67. В обоих случаях ожидаемая прибыль составляет +100 единиц (+10 %).
Мы можем отчетливо наблюдать увеличение отклонения при увеличении коэффициентов (или же при снижении предполагаемой вероятности), что соответствует ранее проведенному анализу. На диаграмме выше показаны результаты для размещения 1000 ставок по 1 единице, с 10%-ным преимуществом, со среднеквадратическим отклонением величиной в 6,5 % и с учетом предположения, что все ставки размещаются с коэффициентами величиной в 5,0; сравнение выполняется с 2,5%-ным преимуществом и коэффициентами в размере 1,67. В обоих случаях ожидаемая прибыль составляет +100 единиц (+10 %).
Интересен также тот факт, что для коэффициентов ниже 2,0 при увеличении преимущества (и, соответственно, ожидаемой прибыли) уменьшается среднеквадратическое отклонение. Нахождение увеличивающегося преимущества для коэффициентов ниже 2,0 вознаграждается не только увеличением ожидаемой прибыли, но и снижением величины отклонения.
Выводы, сделанные на основе собранных данных
В этой статье с помощью симуляции серий ставок с положительным преимуществом исследуются взаимосвязи между коэффициентами, преимуществами и отклонениями.
Несмотря на то, что большая величина преимущества и большее количество ставок увеличивают вероятность справиться с чередой неудач, для игроков, размещающих ставки на исходы спортивных состязаний, важно понимать, к какому типу они относятся, а также уметь рассчитывать величину своего преимущества.
Эти навыки позволят им эффективнее избегать расстройств при череде неудач и не приобретать чрезмерную уверенность в том случае, если исходы для них крайне благоприятны.
Игрок может и не знать точную величину своего преимущества при размещении каждой отдельно взятой ставки: в предыдущих статьях Пиннакл обсуждались причины для использования итоговых коэффициентов Пиннакл в качестве эталона истинных коэффициентов.
Если игрокам удается регулярно зарабатывать на ставках с итоговыми коэффициентами, то у него есть все шансы обеспечить положительный возврат по своим вложениям.
источник pinnacle
Регистрируйся в BYBIT и получи БОНУС БЕЗ ДЕПОЗИТА!

ЗАБРАТЬ БОНУС
(при открытии счета с приложения введите реферальный код NEEDBONUS)
Премиальный USDT Букмекер и Казино с высокой отдачей (99%)

